Ejemplo 1

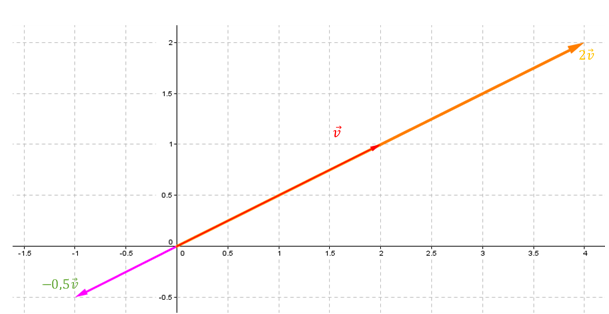
Las combinaciones lineales del vector $\left(2,1\right)$ son todos los vectores de la forma $\left(2k,k\right)$ con $k\in \mathbb{R}$.

Geométricamente el subespacio generado por $\left(2,1\right)$ es la recta que pasa por el origen y tiene la dirección de dicho vector.

Ejemplo 2

Las combinaciones lineales de los vectores $\left(1,0,2\right),\left(0,0,1\right)$ son los vectores coplanares con $\left(1,0,2\right)$ y $\left(0,0,1\right)$:

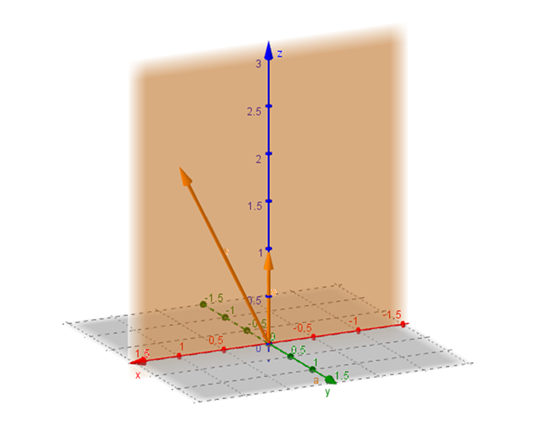
Veamos, analíticamente, cual es el espacio generado por $\left(1,0,2\right),\left(0,0,1\right)$:

$$\left(x,y,z\right)=\alpha \left(1,02\right)+\beta \left(0,0,1\right)=\left(\alpha ,0,2\alpha +\beta \right)\alpha ,\beta \in \mathbb{R}$$

Son todos los vectores con segunda componente nula. Es decir que el subespacio generado es el plano $y=0$.

O sea: $gen\left\{\left(1,0,2\right),\left(0,0,1\right)\right\}=\left\{\left(x,y,z\right)\in {\mathbb{R}}^3:y=0\right\}$

Ejemplo 3

Tomemos los vectores del ejemplo anterior: $\left(1,0,2\right),\left(0,0,1\right)$ y además el vector$\left(-1,0,1\right)$.

¿Qué espacio generan?

$$\left(x,y,z\right)=\alpha \left(1,02\right)+\beta \left(0,0,1\right)+\gamma \left(-1,0,1\right)=\left(\alpha -\gamma ,0,2\alpha +\beta +\gamma \right)$$

Son vectores con segunda componente nula. Se genera el mismo subespacio que en el ejemplo anterior. Esto se explica porque el tercer vector es coplanar con los primeros dos.